what is frame Diagram ?

Definition 

A frame diagram is a generic problem diagram capturing such a problem pattern is called a frame.

Instead of writing problem diagrams from scratch for every problem world we need to delimit, we might predefine a number of frequent problem patterns. A specific problem diagram can then be obtained in matching situations by instantiating the corresponding pattern (Jackson, 2001). This is another illustration of the knowledge reuse technique 

Explanation 

The interface labels are now typed parameters; they are prefixed by 'C', 'E' or 'Y', depending on whether they are to be instantiated to casual, event or symbolic phenomena, respectively. 

A generic component in a frame diagram can be further annotated by its type:

Causal Component

A component marked by a 'C', has some internal causality that can be enforced, e.g. it reacts predictably in response to external stimuli. A machine component is intrinsically causal. 

Biddable Component

 A  component marked by a 'B', has no such enforceable causality, e.g. it consists of people.

Lexical Component

A component, marked by an 'X', is a symbolic representation of data.

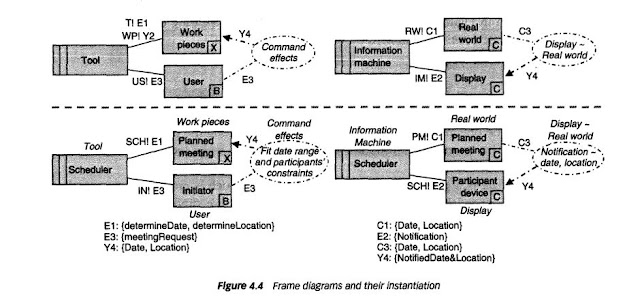
The upper part shows two frame diagrams. The one on the left-hand side represents the Simple Workpieces frame. It captures a problem class where a machine is a tool allowing a user to generate information that can be analysed and used for other purposes. The frame diagram on the right-hand side represents the Information Display frame. It captures a problem class where the machine must present information in a required form to environment components

The frame diagram specifies that the information machine component monitors a causal phenomenon C1 from the RealWorld component and produces an event phenomenon E2 for a Display component as a result. The requirement constraining the latter component is a generic accuracy requirement, as indicated by the ' .....,• symbol; it prescribes that the information displayed should accurately reflect a causal phenomenon C3 from the RealWorld component. 

The lower part shows corresponding frame instantiations yielding problem diagrams. The phenomenon instantiations, compatible with the corresponding p~rameter type, are shown on the bottom. The component instantiations, compatible with the corresponding Component type, are annotated with the name of the generic component to indicate their role in the frame instantiation. For example, the instantiated right-hand side requirement states that the notified meeting date and location must be the one determined by the Scheduler component.

Other frames can be similarly defined and instantiated, for example for problems where the environment behaviours must be controlled by the machine in accordance with commands issued by an operator, or for problems where the machine must transform input data into output data (Jackson, 2001).

Context and problem diagrams provide a simple, convenient notation for delimiting the scope of the system-to-be in terms of components relevant to the problem world and their static interconnections. There is a price to pay for such simplicity. The properties of the interaction between pairs of components are not made precise. The granularity of components and the criteria for a component to appear in a diagram are not very clear either. 

For example

A network component might be part of the problem world of scheduling meetings involving participants who are geographically distributed. According to which precise criteria should this component appear or not. Problem diagrams may also become clumsy for large sets of requirements. 

How do we compose or decompose them? What properties must be preserved under composition or decomposition? we will come back to those issues. A more precise semantics will be given for components and connections, providing criteria for identifying and refining components and interconnections. We will also see there how the / useful view offered by context and problem diagrams can be derived systematically from goal diagrams.